Bases de l’analyse de l’empilement de tolérances: Un guide complet

Voici un cauchemar courant en ingénierie. Un grand lot de pièces fabriquées arrive à votre usine. Vous les inspectez attentivement. Chaque composant individuel mesure parfaitement ses tolérances spécifiées. Alors, Vous commencez l’assemblage, et un problème critique émerge: Les pièces ne s’ajustent pas. Un écart crucial est trop faible, ou un alignement est décalé. Ce scénario frustrant et coûteux résulte presque toujours d’un effet cumulatif appelé empilement de tolérance.

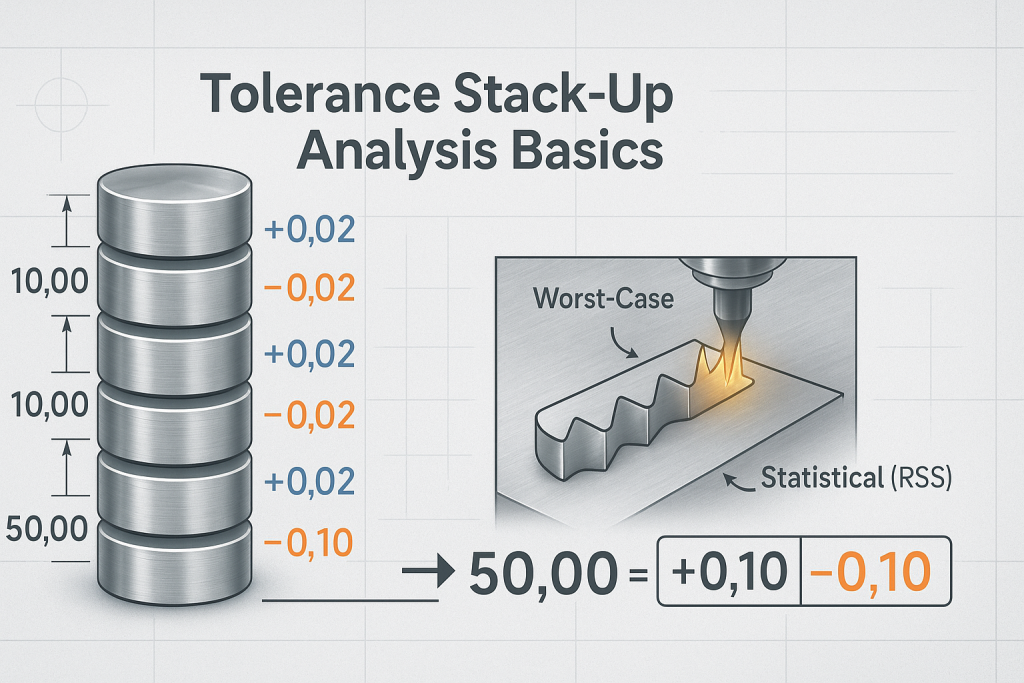
L’analyse d’empilement de tolérances est une méthode d’ingénierie critique utilisée pour calculer l’effet cumulatif des tolérances au niveau des pièces sur un assemblage final. C’est un outil prédictif. Il détermine la variation totale possible d’une dimension critique afin de garantir que les composants s’ajusteront et fonctionneront toujours correctement, Bien avant que le matériau ne soit coupé. C’est un pilier fondamental d’une bonne conception pour la fabricabilité (DFM).

En tant que partenaire de fabrication qui met l’accent sur la DFM, GD-Prototypage travaille avec les clients pour éviter les problèmes d’assemblage avant qu’ils ne surviennent. Ce guide offre une introduction complète aux bases de l’analyse des empilements de tolérances. Nous expliquerons pourquoi c’est essentiel, comment réaliser une analyse 1D, et détaillent les deux méthodes principales pour calculer les résultats.

Le problème de la variation: Pourquoi les tolérances individuelles ne suffisent pas

Pour comprendre l’empilement des tolérances, Il faut d’abord accepter une vérité fondamentale de la fabrication: Aucune partie n’est jamais vraiment identique. Chaque processus de fabrication, de l’usinage CNC au moulage par injection, a un certain degré d’inhérence, variation inévitable. Le but d’une tolérance sur un dessin d’ingénierie est de définir les limites acceptables de cette variation. Une dimension spécifiée comme 20 mm ±0,1 mm signifie que toute pièce mesurant entre 19.9 mm et 20.1 MM est considéré comme un "bon" partie.

Comment les tolérances "Stack Up" dans une assemblée

Le problème survient lorsque ces individus, Les variations acceptables sont combinées dans un assemblage. Imaginez empiler un tas de dix pièces. Chaque pièce individuelle a une faible tolérance d’épaisseur. Une seule pièce peut être légèrement plus épaisse ou plus fine que la valeur nominale. Quand tu empiles dix pièces ensemble, ces petits, Les variations individuelles s’accumulent. La hauteur totale de la pile aura une variation de potentiel bien plus grande que celle de n’importe quelle pièce unique. Les tolérances ont "empilés."

Dans un ensemble mécanique, Le même effet se produit. La position finale d’un composant, ou la taille d’un écart critique, est souvent déterminé par une chaîne de plusieurs dimensions individuelles sur plusieurs parties. Chacune de ces dimensions a sa propre tolérance. L’analyse de stack-up consiste à additionner ces tolérances individuelles le long d’un chemin spécifique afin de trouver la variation totale possible.

L’objectif d’une analyse de stack-up

L’objectif principal d’une analyse de stack-up est de prédire et de gérer cette variation totale. En réalisant cette analyse pendant la phase de conception, un ingénieur peut:

• Assemblage de garantie: Assurez-vous que les pièces s’emboîteront toujours ensemble, peu importe où ils se situent dans leurs bandes de tolérance individuelles.
• Optimiser les tolérances: Identifiez quelles tolérances individuelles aux pièces sont les plus critiques pour l’ensemble. Cela permet à l’ingénieur de resserrer uniquement les tolérances nécessaires, Maintenir les coûts de fabrication bas.
• Réduire les remaniements et la mise au rebut: Évitez le scénario coûteux d’en recevoir des milliers individuellement "bon" Des parties qui aboutissent à "mauvais" Assemblées.

Le "Comment faire": Réalisation d’une analyse d’empilement de tolérance 1D

Une dimension unidimensionnelle (1D) L’empilement est le type d’analyse le plus courant et le plus simple. Il calcule la variation selon un seul, Axe linéaire. Le processus peut être décomposé en cinq étapes claires.

Guide étape par étape

Pas 1: Identifier la dimension critique de l’assemblage D'abord, Identifiez le trou ou l’interface critique que vous devez contrôler. C’est la variable dépendante que vous essayez de calculer. Par exemple, Cela peut être l’espace entre un piston et la paroi du cylindre, ou l’alignement de deux trous de montage.

Pas 2: Créer une chaîne dimensionnelle (ou Chemin de tolérance) En partant d’un côté de la dimension critique, tracez un chemin à travers l’assemblage jusqu’à l’autre côté. Ce chemin ne doit passer que par les dimensions des pièces individuelles qui contribuent directement à la dimension de l’assemblage final. Le chemin doit former une boucle fermée, Commençant et terminant aux deux faces de l’écart critique.

Pas 3: Listez les dimensions et tolérances Créez un tableau simple. Dans ce tableau, Listez chaque dimension individuelle de la pièce incluse dans la chaîne dimensionnelle. À côté de chaque dimension, Listez sa tolérance spécifiée à partir du dessin technique.

Pas 4: Calculer la variation totale C’est l’étape mathématique. Vous appliquerez une méthode spécifique pour additionner les tolérances individuelles de votre liste. Les deux méthodes principales, que nous détaillerons ensuite, sont la méthode du pire cas et la méthode statistique (RSS) méthode.

Pas 5: Comparez le résultat à l’exigence La dernière étape consiste à comparer votre variation totale calculée à la condition fonctionnelle de l’assemblage. Par exemple, Si votre analyse montre qu’un espace critique peut varier de ±0,5 mm, Mais la conception exige qu’il ne dépasse pas ±0,2 mm, Alors votre conception pose un problème. L’ingénieur doit alors retourner à Step 3 et resserrer stratégiquement certaines tolérances individuelles dans la chaîne.

Méthode 1: L’analyse du pire cas

Le pire scénario, ou linéaire, L’analyse est la méthode la plus simple et la plus conservatrice pour calculer l’empilement des tolérances. Il est facile à comprendre et offre une garantie définitive d’assemblage.

Le concept: Préparation au pire scénario

Cette méthode fonctionne sur un point simple, Hypothèse puissante: que toutes les pièces de l’ensemble ont été produites simultanément à leur limite dimensionnelle minimale possible. Il calcule la variation maximale possible en supposant qu’un ensemble de pièces est à son condition matérielle maximale (MMC), et l’autre ensemble est à son condition matérielle minimale (LMC), d’une manière qui maximise l’erreur d’assemblage final.

Le calcul

Le calcul pour la méthode du pire cas est une somme simple. Vous additionnez les valeurs absolues de chaque tolérance individuelle dans la chaîne dimensionnelle.

Variation totale (Pire scénario) = S (toutes les tolérances individuelles)

Un exemple détaillé et travaillé

Analysons un assemblage simple: un arbre qui doit s’insérer dans un boîtier avec un dégagement spécifique, ou "brèche," à la fin.

• Longueur des logements: 50.0 mm ±0,2 mm
• Longueur de l’arbre: 49.0 mm ±0,1 mm
• L’objectif: Calculez la variation totale possible de l’écart entre l’extrémité de l’arbre et l’intérieur du logement.

Pas 1: Dimension critique: Le "Brèche."

Pas 2: Chaîne dimensionnelle: Commencez par la face intérieure du boîtier (Face A). Déplacez-vous le long de la longueur du boîtier jusqu’à la face extérieure (Face B). Reculez le long de la longueur de l’arbre jusqu’à l’extrémité de l’arbre (Face C). Le chemin est terminé.

Pas 3: Dimensions de la liste:

• Longueur des logements: ±0,2 mm
• Longueur de l’arbre: ±0,1 mm

Pas 4: Calculez le pire

• Variation totale = (Tolérance au logement) + (Tolérance d’arbre)
• Variation totale = 0.2 mm + 0.1 mm
• Variation totale = ±0,3 mm

Pas 5: Comparez et interprétez le résultat. L’écart nominal est 50.0 mm - 49.0 mm = 1.0 mm. La variation totale est de ±0,3 mm.

• Maximum Gap: 1.0 mm + 0.3 mm = 1.3 mm (quand le logement est à son plus long et que l’arbre est à son plus court).
• Écart minimum: 1.0 mm - 0.3 mm = 0.7 mm (quand le logement est à son plus court et que l’arbre est à son plus long).

Cette analyse indique à l’ingénieur que cet ensemble aura toujours un espace entre 0.7 mm et 1.3 mm. Si la conception peut fonctionner dans cette plage, Ça marchera 100% de l’époque.

Avantages et inconvénients de la méthode du pire cas

Le principal avantage de cette méthode est qu’elle garantit que 100% des assemblages s’intégreront. C’est une approche sûre et conservatrice. Son principal inconvénient est qu’elle conduit souvent à des tolérances individuelles inutilement strictes et coûteuses. Dans un assemblage complexe, la somme de toutes les tolérances peut devenir très grande, ce qui oblige l’ingénieur à spécifier une précision très coûteuse sur chaque composant.

Méthode 2: Les statistiques (RSS) Analyse

La somme des racines au carré (RSS) La méthode est plus réaliste, et plus complexe, approcher. Il utilise des principes statistiques pour prédire la variation probable dans un assemblage.

Une approche plus réaliste: Somme de racines au carré (RSS)

La méthode RSS repose sur un principe statistique clé: Il est extrêmement improbable que toutes les pièces d’un ensemble atteignent en même temps leur pire limite dimensionnelle possible. Dans un processus de fabrication stable, Les dimensions des pièces suivront une distribution normale, ou "courbe en cloche." La plupart des pièces seront très proches de la dimension nominale, et très peu seront proches des extrêmes de la plage de tolérance. La méthode RSS exploite cette probabilité.

Le calcul

Le calcul pour la méthode RSS consiste à prendre la racine carrée de la somme des carrés de chaque tolérance individuelle.

Variation totale (RSS) = √ (Tolérance₁² + Tolérance₂² + ... + Tolérance n²)

Le même exemple fonctionnait, Recalculé avec RSS

Utilisons le même arbre et le même ensemble de logement.

• Tolérance au logement: ±0,2 mm
• Tolérance d’arbre: ±0,1 mm

Pas 4: Calculer la variation RSS.

• Variation totale = √ ( (0.2)² + (0.1)² )
• Variation totale = √ ( 0.04 + 0.01 )
• Variation totale = √ ( 0.05 )
• Variation totale = ±0,224 mm

Pas 5: Comparez et interprétez le résultat. L’analyse RSS prévoit une variation totale de seulement ±0,224 mm.

• Maximum Gap (Statistique): 1.0 mm + 0.224 mm = 1.224 mm
• Écart minimum (Statistique): 1.0 mm - 0.224 mm = 0.776 mm

C’est une plage de variation bien plus petite que les ±0,3 mm prédits par la méthode du pire des cas.

Avantages et inconvénients de la méthode RSS

Le principal avantage de la méthode RSS est qu’elle permet une plus grande générosité, Tolérances individuelles moins coûteuses. Elle offre une prédiction plus réaliste de la variation de l’assemblage final. Le principal inconvénient est que cela ne garantit pas 100% Succès à l’assemblée. Le calcul RSS standard prédit la variation à ±3 écarts-types (±3S), ce qui correspond à un taux de réussite de 99.73%. Cela signifie que à peu près 2,700 les parties par million pourraient sortir de la fourchette calculée.

Choisir la bonne méthode et agir

Le choix entre ces deux méthodes est une décision stratégique basée sur le profil de risque de l’application et le volume de production.

Quand utiliser le pire cas vs. RSS

• Utiliser la méthode du pire cas pour:
  • Critique, Assemblages à faible volume où la défaillance n’est pas une option. Cela inclut des applications dans l’aérospatiale, Implants médicaux, et systèmes de défense.
  • Assemblages avec très peu de composants, où la différence entre le pire cas et le RSS est faible.
  • Toute situation où un 100% Garantie d’ajustement est requise.
• Utiliser la méthode RSS pour:
  • Produits à fort volume, comme l’électronique grand public ou les composants automobiles. Dans ces cas, Il est plus rentable d’accepter un nombre statistiquement infime d’assemblages hors spécifications que de resserrer la tolérance sur des millions de pièces individuelles.
  • Assemblages comportant un grand nombre de composants dans la chaîne dimensionnelle.

Que faire des résultats

Si l’analyse montre que la variation totale est trop grande pour que l’ensemble fonctionne correctement, L’ingénieur doit agir. Cela implique de revenir à la chaîne dimensionnelle et de resserrer stratégiquement les tolérances sur un ou plusieurs composants individuels. L’analyse permet d’identifier quels composants ont le plus grand impact sur l’empilement, permettant à l’ingénieur d’apporter des améliorations ciblées et rentables. Le choix du procédé de fabrication influence le coût de resserrement de ces tolérances. Référez-vous à notre Tolérances d’usinage CNC et Tolérances de tôle métallique Guides pour plus d’informations.

Conclusion

L’analyse des empilements de tolérance est une conception essentielle pour la fabricabilité (DFM) outil. Il comble le fossé critique entre la conception au niveau des pièces et le succès au niveau de l’assemblage final. En prédisant l’effet cumulatif de la variation manufacturière, Il permet aux ingénieurs de concevoir des assemblages qui s’adaptent et fonctionnent correctement dès la première fois. C’est un processus proactif qui évite des refontes coûteuses, Réduit la ferraille, et assure une transition fluide de la conception à la production.

Que ce soit en utilisant la sécurité absolue de la méthode du pire cas ou le réalisme statistique de la méthode RSS, Réaliser une analyse de stack-up est une caractéristique d’une ingénierie rigoureuse. Au GD-Prototypage, Notre équipe d’experts comprend la relation critique entre les tolérances au niveau des pièces et les performances d’assemblage. Nous travaillons avec nos clients pour garantir que leurs designs soient non seulement fabriquables, mais aussi prêts pour un assemblage parfait.