Grundlagen der Toleranzaufbauanalyse: Ein vollständiger Leitfaden

Hier ist ein häufiger technischer Albtraum. Eine große Charge gefertigter Teile kommt bei Ihnen vor Ort an. Du inspizierst sie sorgfältig. Jedes einzelne Bauteil misst perfekt innerhalb der vorgegebenen Toleranzen. Dann, Sie beginnen mit der Montage, und ein kritisches Problem taucht auf: die Teile passen nicht. Ein entscheidender Abstand ist zu klein, oder eine Ausrichtung ist deaktiviert. Dieses frustrierende und kostspielige Szenario ist fast immer das Ergebnis eines kumulativen Effekts, der als Toleranzstapel bekannt ist.

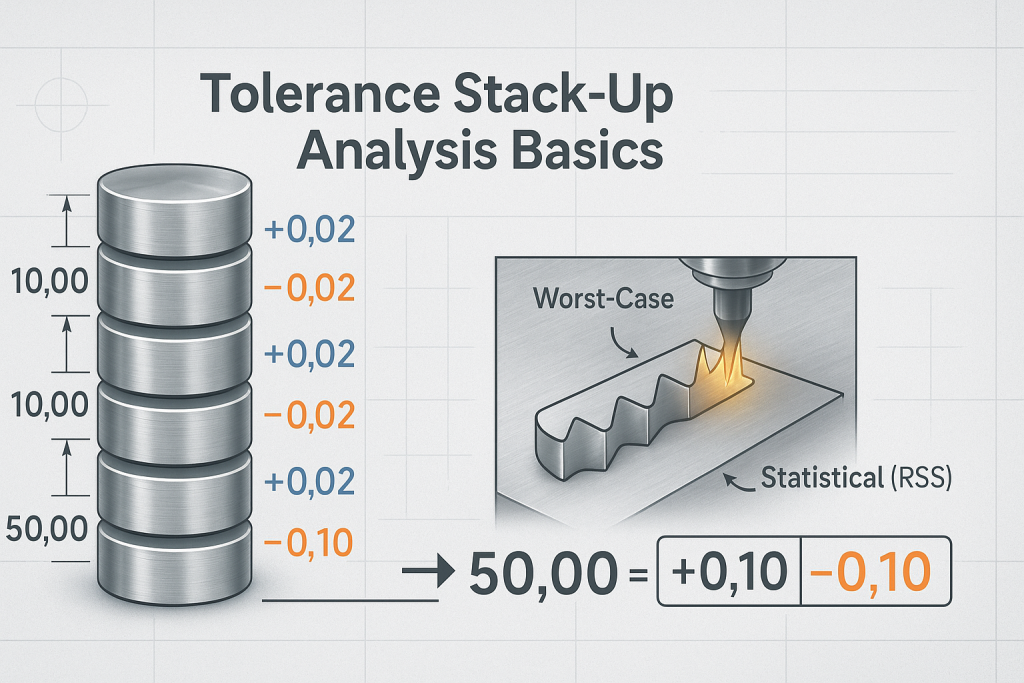
Die Toleranzaufbauanalyse ist eine wichtige technische Methode, die zur Berechnung der kumulativen Auswirkungen von Toleranzen auf Teileebene auf eine Endmontage verwendet wird. Es ist ein Vorhersagewerkzeug. Es bestimmt die insgesamt mögliche Abweichung in einer kritischen Dimension, um sicherzustellen, dass die Komponenten immer passen und korrekt funktionieren, lange bevor irgendein Material geschnitten wird. Es ist eine grundlegende Säule eines guten Design for Manufacturability (DFM).

Als Fertigungspartner, der DFM groß geschrieben hat, GD-Prototyping arbeitet mit Kunden zusammen, um Montageprobleme zu vermeiden, bevor sie entstehen. Dieser Leitfaden bietet eine umfassende Einführung in die Grundlagen der Toleranzaufbauanalyse. Wir erklären Ihnen, warum es wichtig ist, So führen Sie eine 1D-Analyse durch, und beschreiben Sie die beiden Hauptmethoden zur Berechnung der Ergebnisse.

Das Problem der Variation: Warum individuelle Toleranzen nicht ausreichen

So verstehen Sie die Toleranzstapelung, Man muss zuerst eine grundlegende Wahrheit der Fertigung akzeptieren: Keine zwei Teile sind jemals wirklich identisch. Jeder Herstellungsprozess, von der CNC-Bearbeitung bis zum Spritzguss, hat ein gewisses Maß an inhärenter, Unvermeidbare Variation. Der Zweck einer Toleranz in einer technischen Zeichnung besteht darin, die akzeptablen Grenzen dieser Abweichung zu definieren. Eine Dimension, die als 20 mm ±0,1 mm bedeutet, dass jedes Teil, das zwischen 19.9 mm und 20.1 mm gilt als "gut" Teil.

Wie Toleranzen "Aufstapeln" in einer Baugruppe

Problematisch wird es, wenn diese, Akzeptable Abweichungen werden in einer Baugruppe kombiniert. Stellen Sie sich vor, Sie stapeln einen Stapel von zehn Münzen. Jede einzelne Münze hat eine geringe Dickentoleranz. Eine einzelne Münze kann etwas dicker oder dünner als der Nennwert sein. Wenn du zehn Münzen zusammen stapelst, Diese kleinen, Individuelle Variationen häufen sich. Die Gesamthöhe des Stapels weist eine viel größere potenzielle Variation auf als jede einzelne Münze. Die Toleranzen haben "gestapelt."

In einer mechanischen Baugruppe, Derselbe Effekt tritt auf. Die endgültige Position einer Komponente, oder die Größe eines kritischen Spalts, wird oft durch eine Kette von mehreren Einzeldimensionen auf mehreren Teilen bestimmt. Jedes dieser Dimensionen hat seine eigene Toleranz. Bei der Stapelanalyse werden diese einzelnen Toleranzen entlang eines bestimmten Pfads addiert, um die mögliche Gesamtabweichung zu ermitteln.

Das Ziel einer Stack-up-Analyse

Das Hauptziel einer Stapelanalyse besteht darin, diese Gesamtstreuung vorherzusagen und zu verwalten. Indem Sie diese Analyse während der Entwurfsphase durchführen, Ein Ingenieur kann:

• Garantie-Montage: Stellen Sie sicher, dass die Teile immer zusammenpassen, unabhängig davon, wo sie innerhalb ihrer individuellen Toleranzbänder liegen.
• Toleranzen optimieren: Ermitteln Sie, welche Toleranzen der einzelnen Teile für die Baugruppe am kritischsten sind. Dies ermöglicht es dem Ingenieur, nur die notwendigen Toleranzen zu verengen, Herstellkosten niedrig halten.
• Reduzieren Sie Nacharbeit und Ausschuss: Verhindern Sie das kostspielige Szenario, Tausende von einzeln zu erhalten "gut" Teile, die dazu führen, dass "schlecht" baugruppen.

Das "Anleitungen": Durchführen einer 1D-Toleranzaufbauanalyse

Ein eindimensionales (1D) Stack-up ist die gebräuchlichste und einfachste Art der Analyse. Es berechnet die Variation entlang eines einzelnen, Linearachse. Der Prozess lässt sich in fünf übersichtliche Schritte unterteilen.

Eine Schritt-für-Schritt-Anleitung

Schritt 1: Identifizieren der kritischen Baugruppenbemaßung Erste, Identifizieren Sie die kritische Lücke oder Schnittstelle, die Sie kontrollieren müssen. Dies ist die abhängige Variable, die Sie zu berechnen versuchen. Zum Beispiel, Dabei kann es sich um den Abstand zwischen einem Kolben und einer Zylinderwand handeln, oder das Ausrichten von zwei Befestigungslöchern.

Schritt 2: Erstellen einer Bemaßungskette (oder Toleranzpfad) Beginnend bei einer Seite der kritischen Dimension, Verfolgen Sie einen Pfad durch die Baugruppe zur anderen Seite. Dieser Pfad darf nur durch die Abmessungen der Einzelteile verlaufen, die direkt zum Endmaß der Montage beitragen. Der Pfad muss eine geschlossene Schleife bilden, beginnend und endend an den beiden Seiten der kritischen Lücke.

Schritt 3: Auflisten der Abmessungen und Toleranzen Erstellen einer einfachen Tabelle. In dieser Tabelle, Listet alle einzelnen Teileabmessungen auf, die in die Maßkette aufgenommen wurden. Neben jeder Dimension, Listen Sie die angegebene Toleranz aus der technischen Zeichnung auf.

Schritt 4: Berechnen Sie die Gesamtstreuung Dies ist der mathematische Schritt. Sie wenden eine bestimmte Methode an, um die einzelnen Toleranzen aus Ihrer Liste zu summieren. Die beiden Hauptmethoden, die wir im Folgenden näher erläutern werden, sind die Worst-Case-Methode und die Statistische (RSS) Methode.

Schritt 5: Vergleichen Sie das Ergebnis mit der Anforderung Der letzte Schritt besteht darin, Ihre berechnete Gesamtabweichung mit den funktionalen Anforderungen an die Baugruppe zu vergleichen. Zum Beispiel, Wenn Ihre Analyse zeigt, dass ein kritischer Spalt um ±0,5 mm variieren kann, Die Konstruktion verlangt jedoch, dass sie nicht mehr als ±0,2 mm beträgt, Dann hat Ihr Design ein Problem. Der Techniker muss dann zu Schritt zurückkehren 3 und verschärfen strategisch einige der einzelnen Toleranzen in der Kette.

Methode 1: Die Worst-Case-Analyse

Der Worst-Case, oder linear, Die Analyse ist die einfachste und konservativste Methode zur Berechnung des Toleranzaufbaus. Es ist leicht zu verstehen und bietet eine definitive Garantie für die Montage.

Das Konzept: Vorbereitung auf das Worst-Case-Szenario

Diese Methode funktioniert auf einer einfachen, Mächtige Annahme: dass alle Teile in der Baugruppe gleichzeitig an ihrer absolut schlechtesten Maßgrenze gefertigt wurden. Es berechnet die maximal mögliche Abweichung, indem davon ausgegangen wird, dass ein Satz von Teilen seinen maximalen Materialzustand erreicht hat (MMC), und die andere Gruppe befindet sich in der geringsten materiellen Bedingung (LMC), auf eine Weise, die den Endmontagefehler maximiert.

Die Berechnung

Die Berechnung für die Worst-Case-Methode ist eine einfache Summation. Sie addieren die absoluten Werte jeder einzelnen Toleranz in der Maßkette.

Gesamte Variation (Worst-Case) = S (alle individuellen Toleranzen)

Ein detailliertes Arbeitsbeispiel

Analysieren wir eine einfache Baugruppe: eine Welle, die in ein Gehäuse mit einem bestimmten Spiel passen muss, oder "Lücke," am Ende.

• Länge des Gehäuses: 50.0 mm ±0.2 mm
• Länge des Schaftes: 49.0 mm ±0.1 mm
• Das Ziel: Berechnen Sie die gesamte mögliche Variation des Spalts zwischen dem Ende der Welle und der Innenseite des Gehäuses.

Schritt 1: Kritische Dimension: Das "Lücke."

Schritt 2: Maßkette: Beginnen Sie an der Innenseite des Gehäuses (Gesicht A). Bewegen Sie sich entlang des Längenmaßes des Gehäuses zur Außenfläche (Fläche B). Bewegen Sie sich entlang des Längenmaßes der Welle zurück bis zum Ende der Welle (Fläche C). Der Weg ist abgeschlossen.

Schritt 3: Listen-Dimensionen:

• Länge des Gehäuses: ±0,2 mm
• Länge des Schaftes: ±0,1 mm

Schritt 4: Berechnen Sie das Schlimmste

• Gesamte Variation = (Toleranz des Gehäuses) + (Toleranz der Welle)
• Gesamte Variation = 0.2 Mm + 0.1 Mm
• Gesamtabweichung = ±0,3 mm

Schritt 5: Vergleichen und Interpretieren des Ergebnisses. Die nominale Lücke beträgt 50.0 Mm - 49.0 mm = 1.0 Mm. Die Gesamtabweichung beträgt ±0,3 mm.

• Maximaler Abstand: 1.0 Mm + 0.3 mm = 1.3 Mm (wenn das Gehäuse am längsten und die Welle am kürzesten ist).
• Minimaler Abstand: 1.0 Mm - 0.3 mm = 0.7 Mm (wenn das Gehäuse am kürzesten und die Welle am längsten ist).

Diese Analyse teilt dem Ingenieur mit, dass diese Baugruppe immer einen Abstand zwischen 0.7 mm und 1.3 Mm. Wenn das Design innerhalb dieses Bereichs funktionieren kann, Es wird funktionieren 100% der Zeit.

Vor- und Nachteile der Worst-Case-Methode

Der Hauptvorteil dieser Methode besteht darin, dass sie garantiert, dass 100% der Baugruppen passen. Es ist ein sicherer und konservativer Ansatz. Sein Hauptnachteil ist, dass es oft zu unnötig engen und teuren Einzelteiltoleranzen kommt. In einer komplexen Baugruppe, Die Summe aller Toleranzen kann sehr groß werden, Den Ingenieur zwingen, eine sehr kostspielige Präzision für jedes Bauteil anzugeben.

Methode 2: Die Statistik (RSS) Analyse

Die Wurzelsumme zum Quadrat (RSS) Methode ist realistischer, und komplexer, annähern. Es verwendet statistische Prinzipien, um die wahrscheinliche Streuung in einer Baugruppe vorherzusagen.

Ein realistischerer Ansatz: Wurzelsumme zum Quadrat (RSS)

Die RSS-Methode basiert auf einem zentralen statistischen Prinzip: Es ist äußerst unwahrscheinlich, dass alle Teile einer Baugruppe gleichzeitig an ihrer denkbar schlechtesten Maßgrenze angelangt sind. In einem stabilen Herstellungsprozess, Die Abmessungen der Teile folgen einer Normalverteilung, oder "Glockenkurve." Die meisten Teile werden sehr nahe an den Nennabmessungen liegen, und nur sehr wenige werden sich in der Nähe der äußersten Enden des Toleranzbereichs befinden. Die RSS-Methode nutzt diese Wahrscheinlichkeit.

Die Berechnung

Bei der Berechnung für die RSS-Methode wird die Quadratwurzel aus der Summe der Quadrate jeder einzelnen Toleranz gezogen.

Gesamte Variation (RSS) = √ (Toleranz₁² + Toleranz₂² + ... + Toleranzn²)

Das gleiche funktionierende Beispiel, Mit RSS neu berechnet

Lassen Sie uns die gleiche Wellen- und Gehäusebaugruppe verwenden.

• Toleranz des Gehäuses: ±0,2 mm
• Toleranz der Welle: ±0,1 mm

Schritt 4: Berechnen Sie die RSS-Variation.

• Gesamte Variation = √ ( (0.2)² + (0.1)² )
• Gesamte Variation = √ ( 0.04 + 0.01 )
• Gesamte Variation = √ ( 0.05 )
• Gesamtabweichung = ±0,224 mm

Schritt 5: Vergleichen und Interpretieren des Ergebnisses. Die RSS-Analyse prognostiziert eine Gesamtstreuung von nur ±0,224 mm.

• Maximaler Abstand (Statistisch): 1.0 Mm + 0.224 mm = 1.224 Mm
• Minimaler Abstand (Statistisch): 1.0 Mm - 0.224 mm = 0.776 Mm

Dies ist ein viel kleinerer Variationsbereich als die von der Worst-Case-Methode vorhergesagten ±0,3 mm.

Vor- und Nachteile der RSS-Methode

Der Hauptvorteil der RSS-Methode besteht darin, dass sie eine großzügigere, kostengünstigere Einzelteiltoleranzen. Es bietet eine realistischere Vorhersage der Variation der Endmontage. Der Hauptnachteil besteht darin, dass es nicht garantiert 100% Erfolgreiche Montage. Die Standard-RSS-Berechnung prognostiziert die Streuung bei ±3 Standardabweichungen (±3S), was einer Erfolgsquote von 99.73%. Das bedeutet, dass ungefähr 2,700 Teile pro Million könnten außerhalb des berechneten Bereichs liegen.

Die richtige Methode wählen und Maßnahmen ergreifen

Die Wahl zwischen diesen beiden Methoden ist eine strategische Entscheidung, die auf dem Risikoprofil der Anwendung und dem Produktionsvolumen basiert.

Wann sollte Worst-Case vs. verwendet werden?. RSS

• Verwenden Sie die Worst-Case-Methode für:
  • Kritisch, Baugruppen mit geringem Volumen, bei denen ein Ausfall keine Option ist. Dazu gehören auch Anwendungen in der Luft- und Raumfahrt, Medizinische Implantate, und Abwehrsysteme.
  • Baugruppen mit sehr wenigen Bauteilen, wobei der Unterschied zwischen Worst-Case und RSS gering ist.
  • Jede Situation, in der ein 100% Passformgarantie ist erforderlich.
• Verwenden Sie die RSS-Methode für:
  • Produkte mit hohem Volumen, wie Unterhaltungselektronik oder Automobilkomponenten. In diesen Fällen, Es ist kostengünstiger, eine statistisch winzige Anzahl von Baugruppen außerhalb der Spezifikation zu akzeptieren, als die Toleranz bei Millionen von Einzelteilen zu verringern.
  • Baugruppen mit einer großen Anzahl von Komponenten in der Maßkette.

Was tun mit den Ergebnissen?

Wenn die Analyse zeigt, dass die Gesamtstreuung zu groß ist, damit die Baugruppe ordnungsgemäß funktioniert, Der Ingenieur muss Maßnahmen ergreifen. Dabei geht es darum, auf die Maßkette zurückzugehen und die Toleranzen an einem oder mehreren der einzelnen Komponenten strategisch zu verengen. Die Analyse hilft zu identifizieren, welche Komponenten den größten Einfluss auf den Stack-up haben, So kann der Ingenieur gezielte und kostengünstige Verbesserungen vornehmen. Die Wahl des Herstellungsverfahrens wirkt sich auf die Kosten für die Verengung dieser Toleranzen aus. Beziehen Sie sich auf unsere Toleranzen bei der CNC-Bearbeitung und Blech-Toleranzen Leitfäden für weitere Informationen.

Schlussfolgerung

Die Analyse des Toleranzaufbaus ist ein wesentliches Design for Manufacturability (DFM) Werkzeug. Es schließt die kritische Lücke zwischen der Konstruktion auf Teileebene und dem Erfolg auf der Endmontageebene. Durch Vorhersage des kumulativen Effekts von Fertigungsschwankungen, Es ermöglicht Ingenieuren, Baugruppen zu entwerfen, die beim ersten Mal korrekt passen und funktionieren. Es handelt sich um einen proaktiven Prozess, der kostspielige Neukonstruktionen verhindert, reduziert Ausschuss, und sorgt für einen reibungslosen Übergang von der Konstruktion zur Produktion.

Sei es mit der absoluten Sicherheit der Worst-Case-Methode oder dem statistischen Realismus der RSS-Methode, Die Durchführung einer Stack-up-Analyse ist ein Kennzeichen rigoroser Ingenieurskunst. Bei GD-Prototyping, Unser Expertenteam versteht die kritische Beziehung zwischen Toleranzen auf Teileebene und der Montageleistung. Wir arbeiten mit unseren Kunden zusammen, um sicherzustellen, dass ihre Entwürfe nicht nur herstellbar, sondern auch fehlerfrei montiert werden können.