Um Guia Completo para o Gráfico de Chapas Metálicas do Fator K
A precisão é a base da fabricação de chapas metálicas. Toda parte tridimensional, de um suporte simples para um gabinete complexo, começa como um padrão plano bidimensional. A precisão máxima da final, A parte curvada depende inteiramente da precisão desse padrão inicial plano. Uma pergunta comum para os projetistas é como calcular corretamente as dimensões desse padrão plano. A resposta está em entender um único, variável crítica que governa a física da flexão de metal: o Fator K.
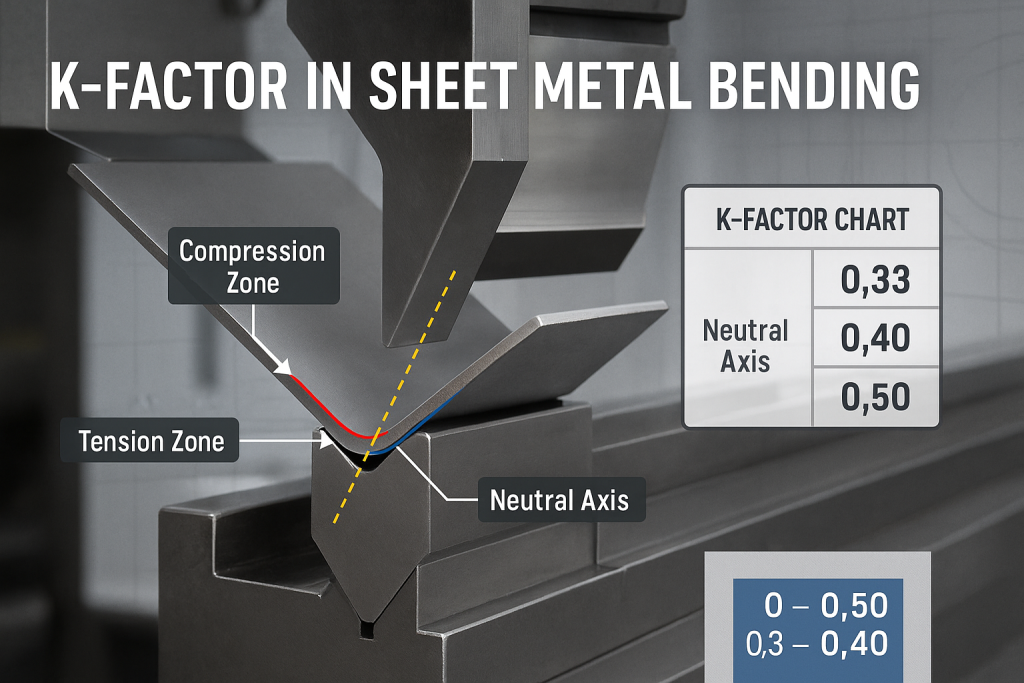
O fator K na chapa metálica é uma razão numérica que define a localização do eixo neutro dentro do material durante uma curvatura. Esse valor, tipicamente entre 0.33 e 0.50, é a variável essencial para calcular com precisão a margem de flexão. É a chave para criar um padrão plano correto que se dobre perfeitamente na geometria 3D desejada.
Como especialistas em fabricação de chapas metálicas de precisão, A GD-Prototipagem depende de cálculos precisos de curvatura para cada projeto. Este guia oferece uma apresentação abrangente, mergulho profundo no K-Factor. Vamos explicar a ciência por trás disso, Como é usado nas fórmulas de dobra de núcleos, e como aplicá-lo em cenários do mundo real.
A Física de uma Curva: Entendendo o Eixo Neutro
Para entender o K-Factor, Primeiro, é preciso entender o que acontece com um pedaço de metal quando ele é dobrado. O processo é mais complexo do que simplesmente dobrar uma folha de papel. Metal é um sólido cristalino, e dobrá-lo força esses cristais a se moverem e deformarem sob pressão imensa.
Compressão e Tensão em uma Curva
Quando uma chapa plana de metal é moldada em uma curva em um freio de pressão, O material é submetido a duas forças opostas.
- O material interno da curvatura é comprimido. O metal é forçado a ocupar um espaço menor, fazendo com que ela aumente levemente de espessura.
- O material na parte externa da curvatura é esticado. O metal é puxado, fazendo com que ela fique um pouco mais fina.
Essa compressão e tensão simultâneas é a dinâmica fundamental da flexão de metais. A superfície externa da curva fica mais longa do que era no estado plano, e a superfície interna fica mais curta.
Definindo o eixo neutro
Em algum lugar entre a superfície interna comprimida e a superfície externa esticada, existe um plano imaginário que não é comprimido nem esticado. Esse plano é conhecido como eixo neutro. O comprimento do eixo neutro permanece constante durante a operação de flexão. Seu comprimento antes da curvatura é o mesmo do comprimento do arco após a curvatura.
Por esse motivo, O eixo neutro é a referência mais importante para todos os cálculos de curvatura. Para criar um padrão plano preciso, devemos calcular o comprimento de arco do eixo neutro através da curvatura. Esse comprimento calculado é o que adicionamos às partes planas da peça para obter o comprimento total do padrão.
Apresentando o K-Factor
O fator K é a variável que nos diz exatamente onde está localizado o eixo neutro. É uma razão simples. Ele representa a distância da face interna do material até o eixo neutro (designado como "t") como fração da espessura total do material (designado como "T").
A fórmula é: K = t / T
Um fator K de 0.50 significa que o eixo neutro está localizado exatamente no centro da espessura do material. Um fator K de 0.33 significa que o eixo neutro está localizado mais próximo da face interna da curva. Na prática, O eixo neutro quase nunca está exatamente no centro. Devido às complexas tensões da flexão, Ele sempre se desloca levemente em direção à superfície interna. Portanto, o K-Factor é quase sempre menor que 0.50.
As Fórmulas Centrais: Allowance por Curvatura e Dedução por Curvatura
O K-Factor não é um número independente; seu único propósito é ser usado dentro das fórmulas centrais que calculam as dimensões de um padrão plano. Os dois conceitos mais importantes neste cálculo são a Permissão por Flexão e a Dedução por Curvatura.
Permissão para Flexão (TRÊS)
A margem de flexão é a aplicação mais direta do fator K. É o comprimento de arco do eixo neutro ao passar pela curvatura. Para calcular o comprimento total de um padrão plano, um projetista adiciona a margem de flexão aos comprimentos das seções planas (As flanges) da parte.
A fórmula para a Permissão de Flexão é: BA = A * (p/180) * (E + K * T)
Onde:
- TRÊS = Permissão para Flexão
- Um = O ângulo de flexão em graus (o ângulo pelo qual o material é dobrado).
- E = O raio interno da curva.
- K = O fator K.
- T = A espessura do material.
Essa fórmula calcula o comprimento exato do material necessário para formar a própria curvatura.
Dedução por Curvatura (BD)
A Dedução por Curvatura é outro método comum usado para calcular o comprimento do padrão plano. Ela aborda o problema de uma perspectiva diferente. Em vez de adicionar a margem de flexão aos comprimentos internos das flanges, Envolve subtrair um valor (a Dedução da Curva) a partir do comprimento total externo da peça.
O cálculo é um pouco mais complexo. Primeiro, requer calcular o "Retrocesso externo" (OSSB), que é a distância do vértice da curvatura até o ponto tangente do raio. A Dedução por Curvatura é então calculada como duas vezes o Retrocesso Externo menos a Tolerância para Flexão.
BD = (2 x OSSB) - TRÊS
Embora ambos os métodos alcancem o mesmo resultado, A margem de flexão é geralmente considerada o método mais direto e intuitivo para entender o papel do fator K. A maioria dos softwares CAD modernos utiliza o K-Factor e a Margem de Curvatura como principais métodos de cálculo.
O Gráfico de Chapas Metálicas do Fator K
O valor do fator K não é constante. Varia de acordo com o tipo de material, sua condição (dureza), e a razão entre o raio de curvatura e a espessura do material. É importante afirmar que qualquer gráfico K-Factor fornece valores iniciais típicos para estimativas de engenharia. O real, O fator K preciso para um conjunto específico só pode ser determinado por meio de testes empíricos com o material e as ferramentas exatas sendo usadas. Contudo, Este gráfico fornece excelentes valores de referência para a fase de projeto.
| Tipo de material | Condição | Raio de Curva (R) / Espessura (T) Relação | Valor do Fator K |
| Alumínio | Macio (Recozido) | R/T < 1.0 | 0.35 |
| 1.0 < R/T < 3.0 | 0.40 | ||
| R/T > 3.0 | 0.50 | ||
| Alumínio | Duro (Por exemplo,, T6 Temper) | R/T < 1.0 | 0.40 |
| 1.0 < R/T < 3.0 | 0.45 | ||
| R/T > 3.0 | 0.50 | ||
| Aço macio | Macio (Recozido) | R/T < 1.0 | 0.42 |
| 1.0 < R/T < 3.0 | 0.46 | ||
| R/T > 3.0 | 0.50 | ||
| Aço inoxidável | Macio (Recozido) | R/T < 1.0 | 0.40 |
| 1.0 < R/T < 3.0 | 0.45 | ||
| R/T > 3.0 | 0.50 | ||
| Aço inoxidável | Duro (Por exemplo,, Full Hard) | R/T < 1.0 | 0.44 |
| 1.0 < R/T < 3.0 | 0.48 | ||
| R/T > 3.0 | 0.50 |
Aplicação Prática: Exemplos Trabalhados
A melhor maneira de entender o K-Factor e a Flexibilidade de Curvatura é passar por um cálculo do mundo real.
Como Usar o K-Factor em um cenário do Mundo Real
Vamos usar as fórmulas e o gráfico para determinar o comprimento correto do padrão plano para um suporte simples em formato de L.
Exemplo 1: Uma curva de 90 graus em aço macio
- Material: 2.0 Aço macio de mm de espessura (Macio)
- Raio de curva interna (E): 2.0 milímetros
- Ângulo de Flexão (Um): 90 Graus
- Flange 1 Comprimento: 50 milímetros
- Flange 2 Comprimento: 30 milímetros
Passo 1: Encontre o K-Factor no gráfico. Primeiro, calculamos a razão R/T.
- R/T = 2.0 milímetros / 2.0 mm = 1.0
- Olhando o gráfico para "Aço macio (Macio)" onde R/T = 1.0, encontramos o O fator K é 0.46.
Passo 2: Calcule a margem de flexão (TRÊS). Agora, inserimos nossos valores na fórmula de Flexibilidade de Curvatura.
- BA = A * (p/180) * (E + K * T)
- BA = 90 * (3.14159 / 180) * (2.0 + 0.46 * 2.0)
- BA = 1.5708 * (2.0 + 0.92)
- BA = 1.5708 * 2.92
- BA = 4.587 milímetros
Passo 3: Calcule o comprimento total do padrão plano. O comprimento total é a soma das seções planas mais a margem de flexão. As seções planas são calculadas a partir dos pontos tangentes da curva, que é o comprimento total da flange menos o raio de curvatura e a espessura.
- Comprimento plano 1 = 50 milímetros - (E + T) = 50 - (2.0 + 2.0) = 46 milímetros
- Comprimento plano 2 = 30 milímetros - (E + T) = 30 - (2.0 + 2.0) = 26 milímetros
- Comprimento Total = Comprimento Plano 1 + Comprimento plano 2 + TRÊS
- Comprimento Total = 46 milímetros + 26 milímetros + 4.587 milímetros
- Comprimento Total do Padrão Plano = 76.587 milímetros
Exemplo 2: Uma curva de 60 graus em alumínio duro
- Material: 3.0 Alumínio Duro de mm de espessura
- Raio de curva interna (E): 6.0 milímetros
- Ângulo de Flexão (Um): 60 Graus
- Flange 1 Comprimento: 40 milímetros
- Flange 2 Comprimento: 40 milímetros
Encontre o K-Factor.
- R/T = 6.0 milímetros / 3.0 mm = 2.0
- Durante "Alumínio duro" onde R/T está entre 1.0 e 3.0, o fator K é 0.45.
Calcule a margem de flexão (TRÊS).
- BA = 60 * (p/180) * (6.0 + 0.45 * 3.0)
- BA = 1.0472 * (6.0 + 1.35)
- BA = 1.0472 * 7.35
- BA = 7.697 milímetros
Calcule o comprimento total do padrão plano.
- Comprimento plano 1 = 40 milímetros - (E + T) = 40 - (6.0 + 3.0) = 31 milímetros
- Comprimento plano 2 = 40 milímetros - (E + T) = 40 - (6.0 + 3.0) = 31 milímetros
- Comprimento Total = 31 milímetros + 31 milímetros + 7.697 milímetros
- Comprimento Total do Padrão Plano = 69.697 milímetros
Fatores que Influenciam o K-Factor na Prática
Os valores no gráfico são excelentes pontos de partida. Contudo, em um ambiente real de fabricação, vários fatores podem fazer com que o fator K real se desvie ligeiramente. Um fabricante de chapa metálica especialista entende essas variáveis e pode ajustá-las para alcançar a máxima precisão.
Por que seu fator K pode ser diferente?
- Propriedades dos materiais: A dureza exata, ductilidade, e a direção dos grãos de um lote específico de metal pode variar ligeiramente do padrão publicado. Um material mais duro terá uma localização diferente no eixo neutro de um mais macio.
- Método de Flexão: A forma como o metal é dobrado tem um impacto significativo. O método mais comum é "Dobra de ar" Em um freio de pressão, onde o punção empurra o metal para dentro de um dado em V sem que ele toque a parte inferior. Um método diferente, "Assentamento," envolve cunhar o material na parte inferior do traço, o que altera as tensões internas e desloca o fator K.
- Ferramental: As ferramentas específicas usadas no freio de pressão são um fator importante. A nitidez do raio do punção e a largura da abertura do chip em V influenciam como o material se deforma e onde o eixo neutro se estabiliza.
- Direção de Curva: A direção da flexão em relação ao veio da chapa metálica também pode causar pequenas variações no Fator K.
Todas essas variáveis do mundo real são consideradas por fabricantes especialistas e são parte fundamental do nosso conjunto abrangente Diretrizes de Projeto de Chapas Metálicas.
O Papel do K-Factor em Software CAD Moderno
Software CAD 3D moderno (como o SolidWorks, Inventor, ou Fusão 360) possui poderosas características de chapa metálica embutidas. Essas ferramentas automatizam o processo de criação de um padrão plano. Contudo, O software não é mágico. Depende do usuário para inserir os parâmetros corretos.
Quando um projetista cria uma peça de chapa metálica em CAD, eles devem definir a espessura do material, O raio interno da curvatura, e um fator de margem de flexão. Esse fator é geralmente o Fator K. O software então utiliza as fórmulas exatas descritas neste guia para calcular automaticamente o padrão plano correto. A precisão da saída do software depende, portanto, completamente da precisão do valor do K-Factor inserido. O uso de um valor padrão genérico pode levar a padrões planos imprecisos e peças que não atendem às suas especificações dimensionais finais. A qualidade final da peça também é impactada pela escolha de Opções de Acabamento em Chapas Metálicas.
Conclusão
O K-Factor é um conceito fundamental na fabricação de chapas metálicas de precisão. É o elo crucial que conecta a peça projetada tridimensionalmente ao padrão plano bidimensional necessário para a fabricação. Embora seja uma proporção simples, Ele representa a física complexa de como o metal se deforma sob pressão. Um fator K correto leva a uma margem de flexão precisa, um padrão plano preciso, e uma parte final que atende a todas as especificações.
Compreender os princípios por trás do K-Factor capacita os engenheiros a criar projetos mais inteligentes e manufáveis. Na GD-Prototiping, Nosso processo de fabricação é construído sobre uma base desses cálculos precisos. Combinamos profundo conhecimento de engenharia com expertise prática para transformar seus projetos complexos em componentes físicos perfeitamente formados.

