Guía completa del gráfico de chapa metálica K-Factor
La precisión es la piedra angular de la fabricación de chapa metálica. Cada parte tridimensional, de un simple corchete a un recinto complejo, comienza como un patrón plano bidimensional. La precisión máxima de la final, La parte doblada depende totalmente de la precisión de este patrón plano inicial. Una pregunta común para los diseñadores es cómo calcular correctamente las dimensiones de este patrón plano. La respuesta está en entender una sola, Variable crítica que rige la física del metal de flexión: el K-Factor.
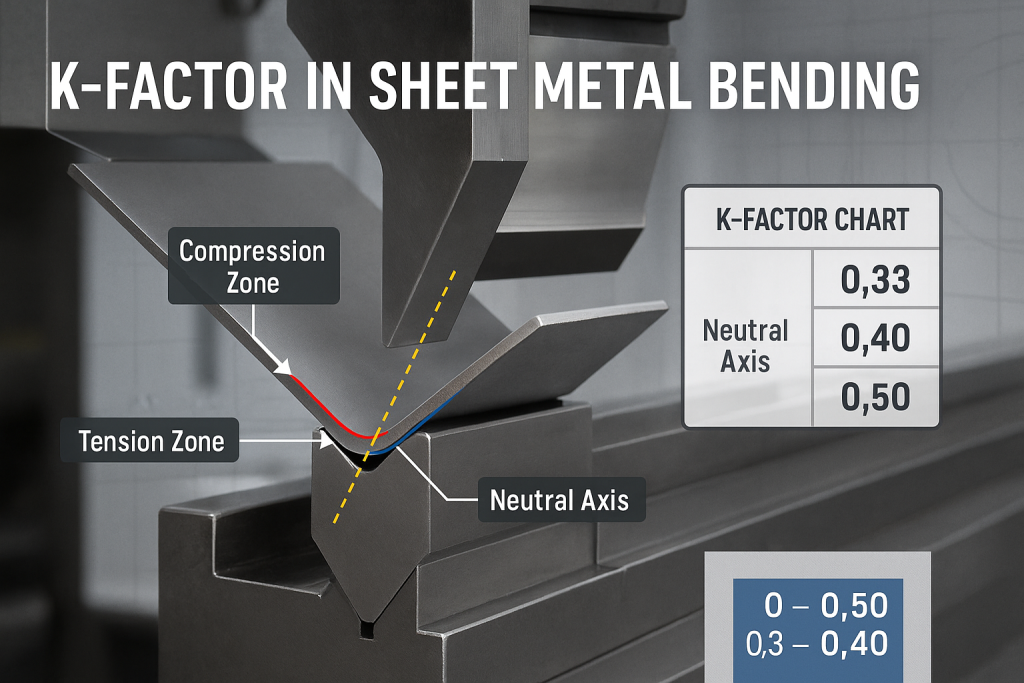
El factor K en la chapa metálica es una relación numérica que define la ubicación del eje neutro dentro del material durante una curvatura. Este valor, típicamente entre 0.33 y 0.50, es la variable esencial para calcular con precisión la margen de flexión. Es la clave para crear un patrón plano correcto que se pliegue perfectamente en la geometría 3D deseada.
Como expertos en fabricación de chapa metálica de precisión, El prototipado GD se basa en cálculos precisos de curvatura para cada proyecto. Esta guía ofrece una visión completa, Profundiza en el K-Factor. Explicaremos la ciencia detrás de ello, Cómo se utiliza en las fórmulas de flexión de núcleos, y cómo aplicarlo en escenarios reales.
La física de una curva: Comprendiendo el eje neutro
Para entender el factor K, Primero hay que entender qué ocurre con un trozo de metal cuando se dobla. El proceso es más complejo que simplemente doblar un trozo de papel. El metal es un sólido cristalino, y doblarlo obliga a estos cristales a moverse y deformarse bajo una presión inmensa.
Compresión y tensión en una curva
Cuando una lámina plana de metal se forma en una curva en un freno de presión, El material está sometido a dos fuerzas opuestas.
- El material en el interior de la curvatura se comprime. El metal se ve obligado a ocupar un espacio más pequeño, lo que hace que aumente ligeramente de grosor.
- El material exterior de la curva se estira. El metal se desmonta, haciendo que se aclare un poco.
Esta compresión y tensión simultáneas es la dinámica fundamental de la flexión del metal. La superficie exterior de la curva se alarga más que en estado plano, y la superficie interior se acorta.
Definición del eje neutro
En algún punto entre la superficie interior comprimida y la superficie exterior estirada, existe un plano imaginario que no está ni comprimido ni estirado. Este plano se conoce como eje neutro. La longitud del eje neutro permanece constante durante la operación de flexión. Su longitud antes de la curva es la misma que su longitud de arco después de la curva.
Por esta razón, El eje neutro es la referencia más importante para todos los cálculos de curvatura. Para crear un patrón plano y preciso, debemos calcular la longitud de arco del eje neutro a través de la curva. Esta longitud calculada es lo que añadimos a las partes planas de la pieza para obtener la longitud total del patrón.
Introducción del K-Factor
El factor K es la variable que nos indica con precisión dónde se encuentra el eje neutro. Es una relación simple. Representa la distancia desde la cara interior del material hasta el eje neutro (designado como "t") como fracción del grosor total del material (designado como "T").
La fórmula es: K = t / T
Un factor K de 0.50 significa que el eje neutro está situado exactamente en el centro del grosor del material. Un factor K de 0.33 significa que el eje neutro está situado más cerca de la cara interior de la curva. En la práctica, El eje neutro casi nunca está exactamente en el centro. Debido a las complejas tensiones de la flexión, Siempre se desplaza ligeramente hacia la superficie interior. Por lo tanto, el K-Factor casi siempre es menor que 0.50.
Las Fórmulas Centrales: Deducción por flexión y deducción por flexión
El K-Factor no es un número independiente; su único propósito es usarse dentro de las fórmulas centrales que calculan las dimensiones de un patrón plano. Los dos conceptos más importantes en este cálculo son la Asignación por Flexión y la Deducción por Flexión.
Asignación por flexión (TRES)
El margen de flexión es la aplicación más directa del factor K. Es la longitud de arco del eje neutro al pasar por la curva. Para calcular la longitud total de un patrón plano, un diseñador añade el margen de flexión a las longitudes de las secciones planas (Las bridas) de la parte.
La fórmula para la Tolerancia de Flexión es: BA = A * (p/180) * (Y + K * T)
Dónde:
- TRES = Permiso de flexión
- A = El ángulo de flexión en grados (el ángulo en que se dobla el material).
- Y = El radio interior de la curva.
- K = El factor K.
- T = El grosor del material.
Esta fórmula calcula la longitud precisa del material necesario para formar la propia curvatura.
Deducción por curva (BD)
La deducción por curva es otro método común utilizado para calcular la longitud del patrón plano. Aborda el problema desde una perspectiva diferente. En lugar de añadir el margen de flexión a las longitudes de la brida interior, implica restar un valor (la deducción de la curva) a partir de la longitud exterior total de la pieza.
El cálculo es algo más complejo. Primero requiere calcular la "Retroceso exterior" (OSSB), que es la distancia desde el vértice de la curvatura hasta el punto tangente del radio. La deducción por flexión se calcula entonces como el doble de la diferencia exterior menos la margen de flexión.
BD = (2 x OSSB) - TRES
Aunque ambos métodos logran el mismo resultado, La margen de flexión se considera generalmente el método más directo e intuitivo para entender el papel del factor K. La mayoría del software CAD moderno utiliza el factor K y la margen de flexión como método principal de cálculo.
La tabla de chapa metálica del factor K
El valor del factor K no es constante. Varía según el tipo de material, su estado (dureza), y la relación entre el radio de curvatura y el grosor del material. Es importante señalar que cualquier gráfico de K-Factor proporciona valores iniciales típicos para estimaciones de ingeniería. El verdadero, El factor K preciso para un montaje específico solo puede determinarse mediante pruebas empíricas con el material y las herramientas exactas que se utilizan. Sin embargo, Este gráfico proporciona excelentes valores base para la fase de diseño.
| Tipo de material | Condición | Radio de curvatura (R) / Espesor (T) Proporción | Valor del factor K |
| Aluminio | Suave (Recocido) | R/T < 1.0 | 0.35 |
| 1.0 < R/T < 3.0 | 0.40 | ||
| R/T > 3.0 | 0.50 | ||
| Aluminio | Duro (P ej.., T6 Temper) | R/T < 1.0 | 0.40 |
| 1.0 < R/T < 3.0 | 0.45 | ||
| R/T > 3.0 | 0.50 | ||
| Acero dulce | Suave (Recocido) | R/T < 1.0 | 0.42 |
| 1.0 < R/T < 3.0 | 0.46 | ||
| R/T > 3.0 | 0.50 | ||
| Acero inoxidable | Suave (Recocido) | R/T < 1.0 | 0.40 |
| 1.0 < R/T < 3.0 | 0.45 | ||
| R/T > 3.0 | 0.50 | ||
| Acero inoxidable | Duro (P ej.., Duro completo) | R/T < 1.0 | 0.44 |
| 1.0 < R/T < 3.0 | 0.48 | ||
| R/T > 3.0 | 0.50 |
Aplicación práctica: Ejemplos Resueltos
La mejor manera de entender el K-Factor y la Asignación de Flexión es recorrer un cálculo real.
Cómo usar el factor K en un escenario real
Vamos a usar las fórmulas y la tabla para determinar la longitud correcta del patrón plano para un corchete simple en forma de L.
Ejemplo 1: Una curvatura de 90 grados en acero dulce
- Material: 2.0 Acero blando de mm de grosor (Suave)
- Radio de curva interior (Y): 2.0 mm
- Ángulo de flexión (A): 90 Grados
- Reborde 1 Largura: 50 mm
- Reborde 2 Largura: 30 mm
Paso 1: Encuentra el factor K en la carta. Primero, calculamos la relación R/T.
- R/T = 2.0 mm / 2.0 mm = 1.0
- Mirando la tabla para "Acero dulce (Suave)" donde R/T = 1.0, Encontramos el El factor K es 0.46.
Paso 2: Calcula la margen de flexión (TRES). Ahora, introducimos nuestros valores en la fórmula de la Flexibilidad de Flexión.
- BA = A * (p/180) * (Y + K * T)
- BA = 90 * (3.14159 / 180) * (2.0 + 0.46 * 2.0)
- BA = 1.5708 * (2.0 + 0.92)
- BA = 1.5708 * 2.92
- BA = 4.587 mm
Paso 3: Calcular la longitud total del patrón plano. La longitud total es la suma de las secciones planas más la margen de flexión. Las secciones planas se calculan a partir de los puntos tangentes de la curva, que es la longitud total de la brida menos el radio de curvatura y el grosor.
- Longitud plana 1 = 50 mm - (Y + T) = 50 - (2.0 + 2.0) = 46 mm
- Longitud plana 2 = 30 mm - (Y + T) = 30 - (2.0 + 2.0) = 26 mm
- Longitud total = longitud plana 1 + Longitud plana 2 + TRES
- Longitud total = 46 mm + 26 mm + 4.587 mm
- Longitud total del patrón plano = 76.587 mm
Ejemplo 2: Una curva de 60 grados en aluminio duro
- Material: 3.0 Aluminio duro de mm de grosor
- Radio de curva interior (Y): 6.0 mm
- Ángulo de flexión (A): 60 Grados
- Reborde 1 Largura: 40 mm
- Reborde 2 Largura: 40 mm
Encuentra el factor K.
- R/T = 6.0 mm / 3.0 mm = 2.0
- Para "Aluminio duro" donde R/T está entre 1.0 y 3.0, el factor K es 0.45.
Calcula la margen de flexión (TRES).
- BA = 60 * (p/180) * (6.0 + 0.45 * 3.0)
- BA = 1.0472 * (6.0 + 1.35)
- BA = 1.0472 * 7.35
- BA = 7.697 mm
Calcular la longitud total del patrón plano.
- Longitud plana 1 = 40 mm - (Y + T) = 40 - (6.0 + 3.0) = 31 mm
- Longitud plana 2 = 40 mm - (Y + T) = 40 - (6.0 + 3.0) = 31 mm
- Longitud total = 31 mm + 31 mm + 7.697 mm
- Longitud total del patrón plano = 69.697 mm
Factores que influyen en el factor k en la práctica
Los valores del gráfico son excelentes puntos de partida. Sin embargo, en un entorno de fabricación real, varios factores pueden hacer que el factor K real se desvíe ligeramente. Un fabricante experto en chapa metálica conoce estas variables y puede ajustarlas para alcanzar la máxima precisión.
¿Por qué podría ser diferente tu factor k??
- Propiedades de los materiales: La dureza exacta, ductilidad, y la dirección del grano de un lote específico de metal puede variar ligeramente respecto al estándar publicado. Un material más duro tendrá una posición diferente en el eje neutro que uno más blando.
- Método de flexión: La forma en que se dobla el metal tiene un impacto significativo. El método más común es "Dominio del aire" Con freno de presión, donde el punzón empuja el metal hacia un chip en V sin que toque el fondo. Un método diferente, "Tocando fondo," consiste en acuñar el material en la parte inferior de la trazada, lo que cambia las tensiones internas y desplaza el factor K.
- Utillaje: El equipo específico utilizado en el freno de presión es un factor importante. La nitidez del radio del punzón y el ancho de la abertura del chip en V influyen en cómo se deforma el material y dónde se asienta el eje neutro.
- Dirección de curva: La dirección de la flexión respecto a la veta de la chapa metálica también puede causar pequeñas variaciones en el factor K.
Todas estas variables del mundo real son consideradas por fabricantes expertos y son una parte clave de nuestro análisis integral Directrices de diseño de chapa metálica.
El papel del K-Factor en el software CAD moderno
Software CAD 3D moderno (como SolidWorks, Inventor, o Fusión 360) cuenta con potentes características de chapa metálica incorporadas. Estas herramientas automatizan el proceso de creación de un patrón plano. Sin embargo, El software no es mágico. Depende de que el usuario introduzca los parámetros correctos.
Cuando un diseñador crea una pieza de chapa metálica en CAD, deben definir el grosor del material, El radio de curvatura interior, y un factor de margen de flexión. Este factor suele ser el factor K. El software utiliza entonces las fórmulas exactas descritas en esta guía para calcular automáticamente el patrón plano correcto. Por tanto, la precisión de la salida del software depende completamente de la exactitud del valor del factor K que se introduce. El uso de un valor genérico por defecto puede dar lugar a patrones planos inexactos y a piezas que no cumplen con sus especificaciones dimensionales finales. La calidad final de la pieza también se ve afectada por la elección de Opciones de acabado en chapa metálica.
Conclusión
El K-Factor es un concepto fundamental en la fabricación de chapa metálica de precisión. Es el eslabón crucial que conecta la pieza diseñada en tres dimensiones con el patrón plano bidimensional necesario para la fabricación. Aunque es una proporción simple, Representa la compleja física de cómo el metal se deforma bajo presión. Un factor K correcto conduce a una margen de flexión precisa, un patrón plano y preciso, y una última parte que cumple con todas las especificaciones.
Comprender los principios detrás del K-Factor permite a los ingenieros crear diseños más inteligentes y fabricables. En GD-Prototipado, Nuestro proceso de fabricación se basa en estos cálculos precisos. Combinamos un profundo conocimiento de ingeniería con experiencia práctica para transformar tus diseños complejos en componentes físicos perfectamente formados.

